- MATEMATİK (limit)

WEBMASTER

EGLENCE

DERSLER

MUZIK


	- MATEMATİK (limit)

Limit kelime Latince Limes ya da Limites 'den gelmekte olup sınır, uç nokta anlamdadır. Öklid ve Arşimet tarafından eğrisel kenarlara sahip şekillerle ilgili olan teoremlerde kullanılmıştır. Limit kavramı, çok önceleri kullanılmasına rağmen sonra unutulmuş ve daha sonra Newton ile Leibniz'in eserlerinde görülmüştür. Mesela, diferansiyel hesapta bir eğri (daire gibi) sonsuz küçük uzunlukta sonsuz kenara sahip bir çokgen olarak kabul edilir. Limit kavramından ortaya çıkan diferansiyel hesap, pekçok fizik probleminin kolayca ele alınmasını sağlar. .

Matematiksel kullanımı

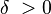f(x) fonksiyonu bir açık aralıkta tanımlanmış olsun, ve L bir gerçel sayı olsun. Bütün $varepsilon >0$ değerleri için, bir $delta >0$ bulunabiliyor, öyle ki bütün 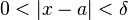$0<|x-a|< delta$ sağlayan $x$ için , $| f (x)-L|< varepsilon$ eşitsizliği doğru ise; L, f(x)'in a noktasındaki limitidir.

Bir fonksiyonun a'daki limiti (L):

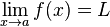
$lim_{x to a}f(x) = L$

şeklinde gösterilir.

Önemli limitler

$lim_{x to infty} (1 + frac {k}{x})^x = e^k$
$lim_{x to 0} (1 + x)^frac {k}{x} = e^k$
$lim_{x to 0} cos(x) = 1$
$lim_{x to 0} frac {sin(x)} {x} = 1$
$lim_{x to 0} frac {tan(x)} {x} = 1$

Limit teoremleri

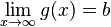Eğer $lim_{x to infty} f(x) = a$ ve $lim_{x to infty} g(x) = b$ ise o zaman aşağidaki denklemler doğru:

$lim_{x to infty} (f(x) pm g(x)) = a pm b$
$lim_{x to infty} (f(x) sdot g(x)) = a sdot b$
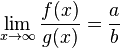$lim_{x to infty} frac {f(x)} {g(x)} = frac {a} {b}$ , eğer $b ne 0$ .
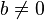Eğer $|f(x)| le |g(x)|$ ve $lim_{x to infty} g(x) = 0$ , o zaman $lim_{x to infty} f(x) = 0$ .