Halka, matematiğin temel yapılarından biridir ve soyut cebirde tam sayıların soyutlamasıdır. Bu yapıyı işleyen dala halka kuramı denir. Halkalara örnek olarak polinomlar, modülo n ya da karmaşık sayılar verilebilir.
Halka her şeyden önce bir kümedir ve belli özellikleri sağlar. Bu özellikler aşağıda verilmiştir.
Tanım
R boştan farklı bir küme olsun. Bu küme üzerinde "+" ve " " ikili işlemleri tanımlı olsun. Eğer;
" ikili işlemleri tanımlı olsun. Eğer;
ise (R,+,  ) kümesine halka denir. Bunların yanında eğer,
) kümesine halka denir. Bunların yanında eğer,
- (R,
 ) kümesi bir birlik ise (R,+,
) kümesi bir birlik ise (R,+,  ) kümesine birimli halka; ayrıca,
) kümesine birimli halka; ayrıca,
- (R,
 ) kümesi değişmeli ise (R,+,
) kümesi değişmeli ise (R,+,  ) kümesine değişmeli halka denir.
) kümesine değişmeli halka denir.
Bir halkanın birinci işlemi olan (genellikle toplama) "+" işleminin birim öğesine sıfır denir ve 0 ile gösterilmesi gelenektir. Halkanın ikinci işlemi olan (genellikle çarpma) " " işleminin birim öğesi varsa bu birim öğeye bir denir ve geleneksel olarak 1 ile gösterilir.
" işleminin birim öğesi varsa bu birim öğeye bir denir ve geleneksel olarak 1 ile gösterilir.
Ayrıca bir halkada genellikle 0=1 olmadığı da bir belit olarak eklenir. Nitekim 1=0 olması bir çelişki yaratmaz ancak, 1=0 olduğunda R halkası tek öğeli bir küme olur. Bunu aşağıdaki gibi basitçe her sayının sıfıra eşit olduğunu göstererek kanıtlayabiliriz:
- a = a.1 = a.0 = 0
Halkanın tam tanımı için bir uzlaşma görülmüyor. Bazı matematikçiler (örneğin Ali Nesin) bir halkanın hem birimli hem bileşmeli hem de değişmeli olduğunu varsayar. Eğer birim öğesiz veya değişme özelliği olmayan bir halkadan bahsedilecekse birimsiz halka ya da değişmesiz halka denmiş olur. Bourbaki ya da Herstein gibi matematikçiler de birim öğesi olmayan halkalara yalancı halka demeyi tercih eder. Bu sayfada bahsedilen halkalar hem değişmeli hem bileşmeli hem de birim öğeli alınacaktır.
Cisim, halka ve öbek gibi soyut bir cebirsel yapıdır. Kabaca, elemanları arasında toplama, çıkarma, çarpma ve bölme (sıfıra bölme hariç) yapılabilen, ve bu işlemlerde sayılardan alışık olduğumuz temel aritmetik kurallarının geçerli olduğu bir küme olarak tanımlanabilir.
Her cisim bir halkadır, fakat bunun tersi geçerli değildir. Mesela tam sayılar kümesi Z bir halka olduğu halde, içinde bölme yapılamadığı için cisim değildir.
Cisimlere örnek olarak, rasyonel sayılar kümesi Q, gerçel sayılar kümesi R ve karmaşık sayılar kümesi C verilebilir. Ayrıca, p bir asal sayı olmak üzere, 0'dan p - 1'e kadar olan tam sayıların kümesi de modüler aritmetik aracılığıyla bir cisim oluşturur. Bu cisim genelde Z/pZ sembolüyle gösterilir.
Tanım
F boş olmayan bir küme olsun, ve bu kümenin elemanları arasında + ve × ile göstereceğimiz iki tane ikili işlem tanımlanmış olsun. (F, +, ×) üçlüsü aşağıdaki şartları sağlıyorsa, bu üçlüyle cisim adı verilir:
 ise,
ise, 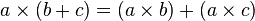 .
.
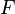 kümesinde
kümesinde  adında öyle bir eleman vardır ki, her
adında öyle bir eleman vardır ki, her 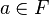 için
için 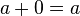 eşitliğini sağlar.
eşitliğini sağlar.
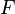 kümesinde
kümesinde  adında,
adında,  'dan farklı öyle bir eleman vardır ki, her
'dan farklı öyle bir eleman vardır ki, her 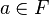 için
için  eşitliğini sağlar.
eşitliğini sağlar.
- Her
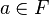 için,
için, 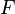 kümesinde
kümesinde  adında öyle bir eleman vardır ki,
adında öyle bir eleman vardır ki, 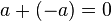 eşitliğini sağlar.
eşitliğini sağlar.
- Her
 için,
için, 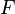 kümesinde
kümesinde  adında öyle bir eleman vardır ki,
adında öyle bir eleman vardır ki,  eşitliğini sağlar.
eşitliğini sağlar.
Tarih
Cisim kavramını ilk ortaya atan Richard Dedekind olmuştur. Dedekind, bu yapı için Almanca'da "cisim" ya da "vücut" anlamına gelen Körper kelimesini kullanmıştır.
